Standing Wave Phenomena
Using Standing Waves to Teach Wave Behavior
Unlike lessons in mechanics or gas laws, which offer many opportunities for hands-on learning, wave behavior can be more difficult to demonstrate. One solution to this challenge is standing wave phenomena. Because of their stationary appearance, standing waves are an ideal system for demonstrating a range of wave topics, including frequency, amplitude, phases, resonance, and harmonics.
Standing waves are most easily observed using a string instrument, such as a guitar, or a tethered string. To create a standing wave, the driving frequency applied to the bound system must equal the natural frequency, a phenomenon known as resonance. While everyday instruments and materials can be a great starting point for standing wave lessons, they rarely provide students with enough detail or control to truly investigate wave behavior.
The PASCO String Vibrator, Sine Wave Generator and Strobe System generate detailed standing wave demonstrations that students can observe, manipulate and measure. Not only are the results amazing, but the demonstration provides a rare opportunity for students to visualize and interact with complex wave phenomena.
The Sine Wave Generator and String Vibrator work together to propagate a sine wave through the rope, while the Strobe System can be used to “freeze” waves in time. As students progress through the standing wave’s harmonics, they can observe the appearance of nodes and antinodes, investigate resonant frequencies, and more.
What is Standing Wave Phenomena?
A standing wave, or stationary wave, occurs when two waves of the same amplitude, frequency and wavelength move in opposite directions. As the waves meet, they become superimposed. This phenomena, known as interference, results in the wave energies being combined or cancelling each other out. If the waves cross with their amplitudes on the same side, then their amplitudes will add together in constructive interference, producing an antinode. Alternatively, if the waves cross with their amplitudes on opposite sides, then the amplitudes will reduce one another, resulting in a smaller net amplitude called a node.
All standing waves have two or more nodes where the wave amplitude equals zero. Between each pair of nodes is a portion of the wave with maximum amplitude, known as an antinode. Antinodes occur when waves of the same phase align and reinforce each other, while nodes occur when waves of opposite phases reduce one another. A Strobe System can be used to enhance the appearance of nodes and antinodes as the wave on the vibrating string transitions through resonant frequencies.
Wave Speed on a Vibrating String
The String Vibrator propagates waves by vibrating a string at the desired frequency. The speed of a wave on a vibrating string is given by the equation:
![]()
Where:
- v is equal to the speed of the wave
- T is equal to the tension in the string
- μ is equal to the linear density
The PASCO solution encourages students to first determine the speed of the string mathematically before comparing their answers to the speed reported by a photogate near the system.
Fundamental Frequency
A stationary wave occurs when the wave oscillates at its lowest frequency, known as the fundamental frequency or fundamental harmonic. For a string of length L, the fundamental harmonic is produced by a vibration whose nodes occur at the two ends of the string. Therefore, the length of the string is equal to half of the wavelength of the fundamental harmonic or frequency. The formula for the fundamental frequency is:
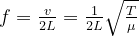
Where:
- T is the tension in Newtons
- μ is the linear density
- L is the length of the vibrating string
- v is the velocity of the string
- f is the frequency of the wavelength
Modes
All systems that support standing wave formations have multiple natural frequencies, known as resonant frequencies. These resonant frequencies, or modes, are equal to integer multiples of the wave’s fundamental frequency. The frequency of the modes can be calculated using the equation:
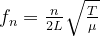
Where:
- T is the tension in Newtons
- μ is the linear density
- L is the length of the string’s vibrating segment
- fn is the frequency of the nth harmonic
The Sine Wave Generator stores the fundamental frequency onboard, enabling users to transition through modes with the press of a button. As students progress through the harmonic series, they can observe the formation of nodes in real time. This highly responsive system allows educators to use it as a live teaching tool that visually demonstrates the behaviors of complex phenomena such as nodes, phases, resonance, and more.
Harmonic Series
The collection of all possible standing wave frequencies for a system is called a harmonic series. The fundamental frequency is the first and simplest harmonic of a system. It has two nodes: one at each end of the string. After the fundamental frequency, all subsequent harmonics are named in order (i.e. second harmonic, third harmonic, etc.). For a vibrating string, such as the one used in our demonstration, the wavelengths of the overtones (harmonics) are equal to ½, ⅓, ¼ and so on of the string’s fundamental wavelength. For more information about harmonics and sound, check out our Sound Waves information guide.
For more information about the PASCO equipment used in this demonstration, select an individual product from the list below.






